2.5 Datenstrukturen Aufgaben
1. Messwert-Erfassung (alpha)
Hinweis (alpha): Aufgabe kann noch Denkfehler enthalten! Bitte auch mit Forsa auf Korrektheit der Darstellung prüfen..
Ein Temperatursensor wird regelmäßig durch eine Steuerung ausgelesen (hier eine vereinfachte Simulation, ich habe auf Timer und GUI verzichtet). Seine Messwerte (Daten) sollen dabei gespeichert und später ausgegeben werden. Drei Datenstrukturen Array, Liste, Schlange werden nun als Lösung zur Datenspeicherung betrachtet.
Ein Klassendiagramm und etwas Code ist schon vorgegeben:
public class Steuerung{
private Sensor derSensor = new Sensor();
private Daten dieDaten = new DatenArray();
//private Timer derTimer = new Timer(this);
public void holeMesswert(){
dieDaten.einfuegenMesswert(new Messwert(derSensor.getTemperatur()));
}
public void testen(){
holeMesswert();
holeMesswert();
holeMesswert();
System.out.print("\f");// Konsole löschen
dieDaten.ausgebenMesswerte();
System.out.println("\nMaximum: "+dieDaten.maxTemperatur());
}
public void testen2(){
holeMesswert();
dieDaten.ausgebenMesswerte();
}
}public class Sensor{
private final static double werte[]={19.3,20.6,21.0,19.7,19.3};
private int index=0;
public double getTemperatur(){
//return Math.round(Math.random()*500)/10.0;
if(index>=werte.length) index=0;
return werte[index++];
}
}public class Messwert{
private double temperatur;
public Messwert(double t){
temperatur=t;
}
public double getTemperatur(){
return temperatur;
}
public String getInfo(){
return "Temperatur: "+temperatur+" °C";
}
}1.1 Klasse DatenArray
Erstellen Sie den Quellcode für die Klasse DatenArray. Neue Messwerte werden am Ende eingefügt.
Lösung
import java.util.ArrayList;
public class DatenArray extends Daten{
private ArrayList<Messwert> dieMesswerte = new ArrayList<>();
public void einfuegenMesswert(Messwert m){
dieMesswerte.add(m);
}
public void ausgebenMesswerte(){
int i;
for(i=0;i<dieMesswerte.size();i++){
System.out.println(dieMesswerte.get(i).getInfo());
}
}
public double maxTemperatur(){
if(dieMesswerte.size()==0) return -99;
int i;
double max=dieMesswerte.get(0).getTemperatur();
for (i=1;i<dieMesswerte.size();i++){
if (dieMesswerte.get(i).getTemperatur()>max)max=dieMesswerte.get(i).getTemperatur();
}
return max;
}
}Erstellen Sie ein Objektdiagramm nach der ersten Ausführung von Steuerung.testen().
Lösung
Erstellen Sie ein Sequenzdiagramm für den Aufruf von Steuerung.testen2().
Lösung
1.2 Klasse DatenListe
Statt DatenArray wird nun die verkettete Liste DatenListe als Datenspeicher verwendet. Neue Messwerte werden am Ende eingefügt.
Erstellen Sie den Quellcode für die Klasse DatenListe und ListKnoten.
Lösung
public class DatenListe extends Daten{
private ListKnoten kopf;
public void einfuegenMesswert(Messwert m){
if (kopf==null){
kopf= new ListKnoten(m);
}
else {
ListKnoten k=kopf;
while (k.getNext()!=null) k=k.getNext(); // bis zum Ende hangeln
k.setNext(new ListKnoten(m));
}
}
public void ausgebenMesswerte(){
if(kopf==null) return;
ListKnoten k = kopf;
while(k!=null){
System.out.println(k.getInhalt().getInfo());
k=k.getNext();
}
}
public double maxTemperatur(){
if(kopf==null) return -99;
ListKnoten k = kopf;
double max=k.getInhalt().getTemperatur();
k = k.getNext();
while(k!=null){
if(max<k.getInhalt().getTemperatur())max=k.getInhalt().getTemperatur();
k=k.getNext();
}
return max;
}
}public class ListKnoten{
private Messwert inhalt;
private ListKnoten next;
public ListKnoten(Messwert m){
inhalt = m;
}
public Messwert getInhalt(){
return inhalt;
}
public ListKnoten getNext(){
return next;
}
public void setNext(ListKnoten k){
next=k;
}
}Erstellen Sie ein Objektdiagramm nach der Ausführung von Steuerung.testen().
Lösung
Erstellen Sie ein Sequenzdiagramm für den Aufruf von Steuerung.testen2().
Lösung
1.3 Bonus: Klasse DatenSchlange
Bei der Operation DatenListe.einfuegenMesswert(m:Messwert) muss sich erst durch die Liste gehangelt werden, bis am Ende ein neuer Messwert eingefügt werden kann. In der Klasse DatenSchlange gibt es deswegen einen Verweis schwanz auf das Ende der Liste.
Erstellen Sie die Operation DatenSchlange.einfuegenMesswert(m:Messwert).
Lösung
public void einfuegenMesswert(Messwert m){
if (kopf==null){
kopf= new ListKnoten(m);
schwanz=kopf;
}
else {
ListKnoten k=new ListKnoten(m);
schwanz.setNext(k);
schwanz=k;
}
}
1.4 Vergleich der Datenstrukturen
Synopsis: [Landau-Symbole]
Der Aufwand zur Speicherung und Verwaltung von n Daten mit einer Datenstruktur wird durch den Speicher- und Rechenaufwand dafür abgeschätzt. Bei einem DatenArray benötigt ein Element einen Verweis somit n Elemente n-Verweise Platz. In einer DatenListe werden pro Element zwei Verweise benötigt.
Der Rechen-(Zeit-)Aufwand ein neues Element hinten einzufügen ist bei einem DatenArray konstant (wenn nicht durch Umkopieren das Array vergrössert werden muss) dafür schreibt man nach O-Notation O(1). Bei einer DatenListe muss erst bis zum Ende gelaufen werden, somit steigt der Aufwand dafür mit der Anzahl n an Elementen, dafür schreibt man O(n).
Füllen Sie die Tabelle aus.
⁈ Welche Datenstruktur würden Sie für die Messwertspeicherung verwenden, begründen Sie Ihre Wahl.
| Bei n vorhandenen Elementen | DatenArray | DatenListe | DatenSchlange |
|---|---|---|---|
| Platzbedarf (Verweise) | |||
| Rechenaufwand einfuegenMesswert() | |||
| Rechenaufwand ausgebenMesswerte() | |||
| Rechenaufwand maxTemperatur() |
Lösung
| Bei n vorhandenen Elementen | DatenArray | DatenListe | DatenSchlange |
|---|---|---|---|
| Platzbedarf (Verweise) | n | 2n | 2n |
| Rechenaufwand einfuegenMesswert() | O(1) | O(n) | O(1) |
| Rechenaufwand ausgebenMesswerte() | O(n) | O(n) | O(n) |
| Rechenaufwand maxTemperatur() | O(n) | O(n) | O(n) |
1.5 Suchbaum?
⁈ Macht es Sinn, als Speicherstruktur einen Suchbaum zu verwenden, begründen Sie ihre Antwort.
Lösung
Nein, denn bei der Anwendung kommt es auf die Reihenfolge der Messwerte und nicht auf die Höhe der Werte an. Ausserdem ergibt sich ein Problem beim Einfügen schon vorhandener Werte z.B. 19.3
ToDo: Interface statt abstrakter Klasse, GUI+Timer?, Portierung als µC-Projekt nach C++ mit Konkretem Sensor…
Steuerungssoftware eines Kaffeevollautomaten (IT-Berufsschulprüfung 21So FIAE)
Synopsis: [Lösung 2021-So-FIA-A1] Ist allerdings eine “Schlange” mit Array und das Klassendiagramm ist noch zu reparieren, Aufgabenidee ist allerdings spannend…
Datenstrukturen im Aufwandsvergleich
Synopsis: [Landau-Symbole] Ich verwende hier eine etwas verfeinerte Darstellung mit Unterstufen O(n/2) zu O(n) und O(log2 n) zu O(log n)
| Bei n vorhandenen Elementen | DatenArray | DatenListe | DatenSchlange |
|---|---|---|---|
| Platzbedarf (Verweise) | |||
| Rechenaufwand Einfügen Vorne | |||
| Rechenaufwand Einfügen Mitte | |||
| Rechenaufwand Einfügen Ende | |||
| Rechenaufwand Suchen unsortiert maximal | |||
| Rechenaufwand Suchen sortiert maximal |
Lösung
| Bei n vorhandenen Elementen | DatenArray | DatenListe | DatenSchlange |
|---|---|---|---|
| Platzbedarf (Verweise) | n | 2n | 2n |
| Rechenaufwand Einfügen Vorne | O(n) | O(1) | O(1) |
| Rechenaufwand Einfügen Mitte | O(n/2) | O(n/2) | O(n/2) |
| Rechenaufwand Einfügen Ende | O(1) | O(n) | O(1) |
| Rechenaufwand Suchen unsortiert maximal | O(n) | O(n) | O(n) |
| Rechenaufwand Suchen sortiert maximal | O(log2 n) (bin. Suche) | O(n)? | O(n)? |
⁈ Vergleichen Sie den Rechenaufwand Einfügen in die Mitte von Array und Verketteter Liste, gehen Sie dabei auf die auszuführenden Aktionen/Operationen ein.
Lösung
Bei einem Array ist der Einfügeort mit einer Rechnung gefunden, nachfolgend müssen n/2 Elemente nach hinten verschoben werden um Platz zu schaffen, somit ist der Aufwand O(n/2). Bei der Liste muss ich erst bis zur Mitte durchgehangelt werden, dies benötigt n/2 Aktionen, das Einfügen benötigt immer gleich lang, somit gilt O(n/2).
SO. (Kartoffel-) Sack-Optimierer (alpha)
Synopsis: [Richtlinie 76/211/EWG (Fertigpackungsrichtlinie)]
Hobby-Biobauer Mezger will seine Feldfrüchte, z.B. Kartoffeln optimal in Säcke verpacken. Die Feldfrüchte haben ein recht unterschiedliches Gewicht, letztlich soll z.B. ein 1 kg Sack möglichst genau (die Abweichung darf bei 500g..1000g maximal ±15g sein) befüllt werden. Zu diesem Zweck werden die Feldfrüchte gewogen und mit auf 10g gerundeten Gewicht in Behälter sortiert. Aus diesen Behältern soll der Sack zusammen gestellt werden. Nun kennt er noch nicht die Bandbreite der Gewichte und möchte auch nicht unzählige Behälter vorhalten. Deshalb will er erst dann einen Behälter anlegen, wenn eine Feldfrucht mit entsprechendem Gewicht beim Wiegen auftaucht. Als mögliche Datenstrukturen stehen verkettete Liste und Suchbaum zur Auswahl.
1 Klasse Feldfrucht
Die Objekte der Klasse Feldfrucht stehen für die Behälter in denen Feldfrüchte mit dem gleichen Gewicht (auf 10g gerundet) gesammelt werden. Z.B. Früchte mit einem Gewicht von 5g..14g werden im Behälter für 10g gesammelt. Das Attribut anzahl:GZ gibt an, wie viele Früchte im Behälter sind. Grundsätzlich darf das Gewicht einer Feldfrucht nicht <1 und die Anzahl nicht <0 sein, siehe Zusicherung. Der Konstruktor setzt das Gewicht auf mindestens 1g und die Anzahl auf 1. Bei Veränderung der Anzahl wird darauf geachtet, dass diese nicht negativ werden kann.
1.1 🖥 Erstellen Sie den Quellcode der Klasse Feldfrucht bis auf die getInfo-Operationen.
Lösung
public class Feldfrucht{
private int gewicht; // {>=1}
private int anzahl; // {>=0}
public Feldfrucht(int g){
if(g<1) g=1; // Minimalgewicht ist 1
gewicht=g;
anzahl=1;
}
public int getGewicht(){
return gewicht;
}
public int getAnzahl(){
return anzahl;
}
public void setAnzahl(int n){
if(n<0) n=0; // Minimalanzahl ist 0
anzahl=n;
}
// nicht verlangt
public String getInfo(){
return String.format("Behälter: %3dg Anzahl: %3d",gewicht,anzahl);
}
public String getInfoKurz(){
return String.format("%2d:%2d",gewicht,anzahl);
}
}2 Feldfrüchte einfügen
Die Operation einfuegenFeldfrucht(g:GZ) der Klasse Daten fügt eine Feldfrucht mit dem Gewicht g in die Datenstruktur ein. Falls noch kein Behälter (Knoten und Frucht-Objekt) für eine Feldfrucht existiert wird er angelegt und eine Frucht hineingelegt. Sonst wird das Attribut anzahl eines vorhandenen Fruchtbehälters um 1 erhöht. Die Operation einfuegenAusStringliste(s: Text) der Klasse Steuerung dient zum Testen.
2.1 Feldfrüchte in DatenListe einfügen
Mit einfuegenAusStringliste(“22 11 33”) wird in vereinfachter Darstellung diese Struktur erzeugt, die Gewichte werden vor dem Einfügen auf 10g gerundet, neue Elemente werden hinten eingefügt:
2.1.1 🖌 Erstellen Sie in vereinfachter Darstellung die Struktur für einfuegenAusStringliste(“81 120 49 76 100”), beachten Sie das Runden auf 10g.
Lösung
2.1.2 🖌 Erstellen Sie ein Objektdiagramm dazu.
Lösung
2.1.3 ⁈ Eine neue Feldfrucht mit Gewicht 140g soll eingefügt werden, wie viele Vergleiche müssen dafür ausgeführt werden? Wie groß ist der Aufwand in O-Notation?
Lösung
Es müssen 4 Vergleiche ausgeführt werden. Der Aufwand ist O(n).
2.1.4 🖥 Erstellen Sie den Quellcode für einfuegenFeldfrucht(g:GZ) der Klasse DatenListe.
Lösungsvorschlag
Fallunterscheidung
- Kopf == null? -> Neue Feldfrucht einfügen, Ende
- Knoteninhalt == g? -> Erhöhe Anzahl um 1, Ende
- Nächster Knoten nicht vorhanden? Neue Feldfrucht einfügen, Ende
- Weiter bei 2. mit nächstem Knoten
public void einfuegenFeldfrucht(int g){ // Aufg 2.1.4 hinten einfuegen
if(kopf == null){
kopf=new ListKnoten(new Feldfrucht(g));
return;
}
ListKnoten k = kopf;
while(true){
if(k.getInhalt().getGewicht()==g){ // ist schon Lager mit h da?
k.getInhalt().setAnzahl(k.getInhalt().getAnzahl()+1);
return;
}
if(k.getNext()==null){ // kommt nix mehr?
k.setNext(new ListKnoten(new Feldfrucht(g))); // einfuegen
return;
}
k=k.getNext(); // naechtes anschauen
}
}2.2 Feldfrüchte in DatenBaum einfügen
Mit einfuegenAusStringliste(“22 11 33”) wird in vereinfachter Darstellung diese Struktur erzeugt, die Gewichte werden vor dem Einfügen auf 10g gerundet, neue Elemente werden sortiert eingefügt, der Baum wird dabei nicht ausbalanciert:
2.2.1 🖌 Erstellen Sie in vereinfachter Darstellung die Struktur für einfuegenAusStringliste(“81 120 49 76 100”), beachten Sie das Runden auf 10g.
Lösung
2.2.2 🖌 Erstellen Sie ein Objektdiagramm dazu.
Lösung
2.2.3 ⁈ Eine neue Feldfrucht mit Gewicht 140g wird eingefügt, wie viele Vergleiche müssen dafür ausgeführt werden?
Lösung
Es müssen 2 Vergleiche ausgeführt werden.
2.2.4 ❓ Welche Höhe hat der Baum nun? Welche Tiefe hat der Knoten 140?
Lösung
Der Baum hat die Höhe 2 (Länge des längsten Pfades von der Wurzel zu einem Blatt). Der Knoten 140 hat die Tiefe 2 (Länge des Pfades bis zur Wurzel). Pfadlänge ist die Anzahl der Kanten.
2.2.5 🖥 Erstellen Sie den Quellcode für einfuegenFeldfrucht(g:GZ) der Klassen DatenBaum und BaumKnoten für einem rekursiven Ansatz.
Lösungsvorschlag
// DatenBaum
public void einfuegenFeldfrucht(int g){
if (wurzel==null){
wurzel = new BaumKnoten (new Feldfrucht(g));
}
else wurzel.einfuegenFeldfrucht(g);
}
// BaumKnoten
public void einfuegenFeldfrucht(int g){ // sortiertes Einfuegen
if(inhalt.getGewicht()==g){
inhalt.setAnzahl(inhalt.getAnzahl()+1);
}
else{
if(g < inhalt.getGewicht()){
if(linkerTeilbaum==null){
linkerTeilbaum= new BaumKnoten(new Feldfrucht(g));
}
else linkerTeilbaum.einfuegenFeldfrucht(g);
}
else{
if(rechterTeilbaum==null){
rechterTeilbaum= new BaumKnoten(new Feldfrucht(g));
}
else rechterTeilbaum.einfuegenFeldfrucht(g);
}
}
}3 Operation getMaxGewicht():GZ
Erstellen Sie den Quellcode für getMaxGewicht():GZ für diese Klassen:
3.1 🖥 DatenListe
Lösungsvorschlag
public int maxGewicht(){ // Aufg 3.1
if(kopf==null) return 0;
ListKnoten k = kopf;
int max=k.getInhalt().getGewicht();
k = k.getNext();
while(k!=null){
if(max<k.getInhalt().getGewicht())max=k.getInhalt().getGewicht();
k=k.getNext();
}
return max;
}3.2 🖥 DatenBaum und BaumKnoten rekursiv
Lösungsvorschlag
// Klasse Datenbaum
public int maxGewicht(){ // Aufg 3.2
if(wurzel==null) return 0;
return wurzel.maxGewicht();
}
// Klasse BaumKnoten
public int maxGewicht(){ // Aufg 3.2
if(rechterTeilbaum==null) return inhalt.getGewicht();
return rechterTeilbaum.maxGewicht();
}4 Operation getGesGewicht():GZ
Erstellen Sie den Quellcode für getGesGewicht():GZ für diese Klassen:
4.1 🖥 DatenListe
Lösungsvorschlag
public int getGesGewicht(){ // Aufg 4.1
if(kopf == null)return 0;
ListKnoten k = kopf;
int sum=0;
while(k!=null){
sum+=k.getInhalt().getGewicht()*k.getInhalt().getAnzahl();
k=k.getNext();
}
return sum;
}4.2 🖥 DatenBaum und BaumKnoten rekursiv
Lösungsvorschlag
// Klasse DatenBaum
public int getGesGewicht(){ // Aufg 4.2
if(wurzel==null) return 0;
return wurzel.getGesGewicht();
}
// Klasse BaumKnoten
public int getGesGewicht(){ // Aufg 4.2
int sum=inhalt.getGewicht()*inhalt.getAnzahl();
if(rechterTeilbaum!=null) sum+= rechterTeilbaum.getGesGewicht();
if(linkerTeilbaum!=null) sum+= linkerTeilbaum.getGesGewicht();
return sum;
}4.3 🖥 DatenBaum getGesGewicht():GZ interativ (siehe Preorder-Ausgabe interativ)
Lösungsvorschlag
public int getGesGewicht(){ // Aufg 4.3
if(wurzel==null) return 0;
Deque<BaumKnoten> stack = new ArrayDeque<BaumKnoten>();
int sum=0;
BaumKnoten k;
stack.push(wurzel);
while(!stack.isEmpty()){
k=stack.pop();
if(k.gibRechtenTeilbaum()!=null) stack.push(k.gibRechtenTeilbaum());
if(k.gibLinkenTeilbaum()!=null) stack.push(k.gibLinkenTeilbaum());
sum += k.getInhalt().getGewicht()*k.getInhalt().getAnzahl();
}
return sum;
}5 Operation getBestFrucht(g:GZ):Feldfrucht (anspruchsvoll)
Beim Befüllen der Säcke werden aus den Behältern passende Feldfrüchte entnommen. Die Operation getBestFrucht(g:GZ):Feldfrucht sucht den nicht leeren Behälter dessen Feldfrüchtegewicht kleiner gleich dem gesuchten Gewicht g ist oder falls dies nicht möglich ist die kleinste Frucht mit g>Fruchtgewicht.
- Gehe alle Behälter durch (Iteration)
- Wenn nicht leerer Behälter mit passendem Gewicht g gefunden wird, gib Verweis auf Behälter zurück (Stopp).
- Merke dir dabei das Gewicht und Verweis des schwersten Behälters, der nicht leer ist und dessen Gewicht kleiner gleich g ist.
- Merke dir dabei das Gewicht und Verweis des leichtesten Behälters, der nicht leer ist und dessen Gewicht größer g ist.
- gib den Verweis des leichteren Behälters zurück.
Erstellen Sie den Quellcode für die Operation getBestFrucht(g:GZ):Feldfrucht der Klassen:
5.1 🖥 DatenListe
Lösungsvorschlag
public Feldfrucht getBestFrucht(int g){ // Aufg 5.1
if(kopf == null) return null;
ListKnoten k = kopf;
Feldfrucht fruchtMaxKG= null; // größte Frucht mit gewicht<=g
int maxKG=0;
Feldfrucht fruchtMinG= null; // kleinste Frucht mit gewicht>g
int minG=Integer.MAX_VALUE;
while(k!=null){
if(g==k.getInhalt().getGewicht() && k.getInhalt().getAnzahl()>0) return k.getInhalt();
if(k.getInhalt().getGewicht()<=g && k.getInhalt().getAnzahl()>0 && k.getInhalt().getGewicht()>maxKG){
fruchtMaxKG=k.getInhalt();
maxKG=fruchtMaxKG.getGewicht();
}
if(k.getInhalt().getGewicht()>g && k.getInhalt().getAnzahl()>0 && k.getInhalt().getGewicht()<minG){
fruchtMinG=k.getInhalt();
minG=fruchtMinG.getGewicht();
}
k=k.getNext();
}
if(fruchtMaxKG!=null) return fruchtMaxKG;
return fruchtMinG;
}5.2 🖥 DatenBaum iterativ (Preorder-Durchlauf)
Lösungsvorschlag
public Feldfrucht getBestFrucht(int g){ // Aufg 5.2 Baum in Preoder durchsuchen
if(wurzel==null) return null;
Deque<BaumKnoten> stack = new ArrayDeque<BaumKnoten>();
BaumKnoten k;
Feldfrucht fruchtMaxKG= null; // größte Frucht mit gewicht<=g
int maxKG=0;
Feldfrucht fruchtMinG= null; // kleinste Frucht mit gewicht>g
int minG=Integer.MAX_VALUE;
stack.push(wurzel);
while(!stack.isEmpty()){
k=stack.pop();
if(k.gibRechtenTeilbaum()!=null) stack.push(k.gibRechtenTeilbaum());
if(k.gibLinkenTeilbaum()!=null) stack.push(k.gibLinkenTeilbaum());
if(g==k.getInhalt().getGewicht() && k.getInhalt().getAnzahl()>0) return k.getInhalt();
if(k.getInhalt().getGewicht()<=g && k.getInhalt().getAnzahl()>0 && k.getInhalt().getGewicht()>maxKG){
fruchtMaxKG=k.getInhalt();
maxKG=fruchtMaxKG.getGewicht();
}
if(k.getInhalt().getGewicht()>g && k.getInhalt().getAnzahl()>0 && k.getInhalt().getGewicht()<minG){
fruchtMinG=k.getInhalt();
minG=fruchtMinG.getGewicht();
}
}
if(fruchtMaxKG!=null) return fruchtMaxKG;
return fruchtMinG;
}Ich bin zu müde eine rekursive Lösung für Baum zu finden 😉 Alternativ zum oberen Algorithmus könnte auch einfach die Frucht mit dem nächstgelegenen Gewicht genommen werden, als geiziger Bauer wollte ich mich jedoch “von unten” möglichst genau an das Sackgewicht anschleichen und nur im Notfall das nächst grössere Ding verwenden. Müsste man untersuchen..
6 Operation entferneLeereBehaelter() der Klasse DatenListe
Ein neues Feld ergibt andere Fruchtgrößen, daher sollte bei den Behältern aufgeräumt werden..
6.1 ✍️ (🖌) Beschreiben Sie wie leere Behälter aus der DatenListe entfernt werden können, Sie dürfen auch eine Zeichnung zur Erläuterung beifügen.
Lösung
Drei Fälle sind zu beachten:
- Kopf ist null -> Ende
- Kopfelement soll gelöscht werden, setze kopf auf kopf.next
- Knotennachfolger soll gelöscht werden, setze knoten.next auf knoten.next.next
6.2 🖥 Erstellen Sie den Quellcode für die Operation entferneLeereBehaelter() der Klasse DatenListe, die leere Behälter aus der Liste entfernt.
Lösungsvorschlag
public void entferneLeereBehaelter(){
if(kopf == null)return;
if(kopf.getInhalt().getAnzahl()==0){ // ersten Knoten löschen
kopf = kopf.getNext();
}
ListKnoten k = kopf;
while(k!=null){
if(k.getNext()==null) return; // Ende der Liste
if(k.getNext().getInhalt().getAnzahl()==0){
k.setNext(k.getNext().getNext());
}
k=k.getNext();
}
}7 Operation gibToleranz(g:GZ):GZ der Klasse Daten
Die Operation gibToleranz(g:GZ):GZ soll nach der Verpackungrichlinie die Gewichtstoleranz beim Zusammenstellen des Sacks ermitteln.
7 🖥 Erstellen Sie den Quellcode.
Lösung
public int gibToleranz(int g){
if(g<50) return (int) (g*0.09);
if(g<100) return 4;
if(g<200) return (int) (g*0.045);
if(g<300) return 9;
if(g<500) return (int) (g*0.03);
if(g<1000) return 15;
return (int) (g*0.015);
}| von (g oder ml) | bis (g oder ml) | maximale Abweichung in % des angegebenen Packungsinhalts | maximale Abweichung absolut (g oder ml) |
|---|---|---|---|
| 5 | 50 | 9,0 | – |
| 50 | 100 | – | 4,5 |
| 100 | 200 | 4,5 | – |
| 200 | 300 | – | 9,0 |
| 300 | 500 | 3,0 | – |
| 500 | 1000 | – | 15 |
| 1000 | 10000 (sonst) | 1,5 | – |
8 Operation ausgebenSack(g:GZ) der Klasse Daten
Die Operation ausgebenSack(g:GZ) gibt zuerst die Toleranz zu dem Zielgewicht des Sacks aus. Der erste einfachste Ansatz zum optimal befüllten Sack geht so:
Solange der Sack noch unter der Toleranz befüllt ist suche mit getBestFrucht(g) und lege Frucht in Sack (Ausgabe auf Konsole).
8 🖥 Erstellen Sie den Quellcode für die Operation ausgebenSack(g:GZ) der Klasse Daten.
Lösungsvorschlag
public void ausgebenSack(int g){ // Aufg 8
int toleranz = gibToleranz(g);
System.out.printf("\nSack mit %3dg ausgeben, Toleranz: +- %2dg\n",g,toleranz);
String s="";
if(g>getGesGewicht()) System.out.println("Nicht genug Ware vorhanden");
else{
int ausgeben = g;
while(ausgeben>toleranz){
Feldfrucht b=getBestFrucht(ausgeben); // grösste Dinger
if(b!=null){
s+=b.getGewicht()+" ";
ausgeben-=b.getGewicht();
b.setAnzahl(b.getAnzahl()-1);
}
else{
System.out.println("Nicht lösbar");
return;
}
}
System.out.println(s);
System.out.printf("Soll: %3d Ist: %3d Abweichung: %2d\n",g,g-ausgeben,-ausgeben);
}
}Der Algorithmus ist nicht optimal, es gibt Fälle in der ein geschickteres Zusammenklauben von Früchten ein genaueres Ergebnis erbringen könnte…
9 Maximale Abweichung vom Zielgewicht ermitteln
⁈ Die Früchte werden auf 10g gerundet in die Behälter abgelegt, somit ergibt sich ein Fehler. Wie groß die die maximale Abweichung in g bei 5 Früchten nach unten und oben, Herleitung!
Lösung
Betrachte Fall 10g Behälter, in ihm sind Früchte von 5,0g..14,9g. Angenommen es sollen 50g ausgegeben werden und dazu 5 Früchte á 10g verwendet. Das geringste Gewicht wäre dabei 5*5g=25g und das höchste Gewicht 5*14,9g = 74,..g. Max. Abweichung ist ±5*5g = ±25g
10 Nachwiegen Sequenzdiagramm
Um das Ziel-Sackgewicht genauer erreichen zu können wird der Sack nun nur bis 90% Zielgewicht aus den Behältern befüllt und gewogen. Der fehlende Rest wird dann wieder mit ausgebenSack nachgelegt.
Vervollständigen Sie das Sequenzdiagramm auf dem Arbeitsblatt…
11 Baum sinnvoll?
Bringt der Suchbaum einen Gewinn gegenüber der Verketten Liste? Betrachten Sie den Aufwand fürs Einfügen von Früchten. Betrachten Sie den Aufwand für das Finden der besten Frucht…
BlueJ Lösung für das Projekt
Projekt SimLive (Scrum)
Verschiedene Arten Spinnen rennen in einer Box rum und fressen Fliegen und sich gegenseitig. Achtung Suchtpotenzial! . Das alte Projekt aus 2006 habe ich nun wieder ausgebuddelt und ein wenig erweitert, z.B. die Zeit zu messen die es braucht alle Viecher rechnerisch “leben” zu lassen. Allerdings sind viele verwendete Klassen veraltet und das Programm hat Bugs.
Z.B. Java-Klasse Vector ist veraltet und sollte durch bessere Datenstruktur ersetzt werden. Endlich mal eine sinnvolle Möglichkeit für verkettete Listen? Es gibt viel zu tun..
Den vorhandenen Code analysieren, diese Klassen ersetzen:
- Vector
- Durch ArrayList?
- Durch verkettete Liste (LinkedList)?
- Bildausgabe für die Spinnen verbessern..
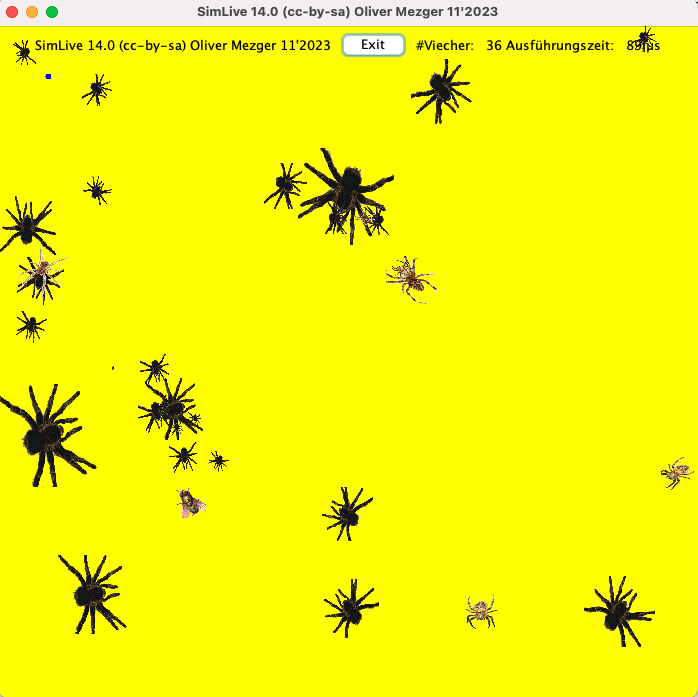
Sprint-Backlog
Es gelten die üblichen Edu-Scrum-Projektregeln. Sie sollen die OOP-Werkzeuge und Datenstrukturen bei einem Projekt anwenden und vertiefen. Für die Diagramme wählen Sie geeignete Szenarien aus Ihrem Projekt aus.
- Mindestens eine der Datenstrukturen verwenden: Verkettete Liste, Baum, Stack, Queue
- Ein Klassendiagramm vom Projekt erstellen, nur die wesentlichen Klassen, Klassenaufteilung erklären, begründen können.
- Ein Zustandsdiagramm erstellen, z.B. die Viecher sind hungrig, müde, auf Jagt, ängstlich usw.
- Ein Sequenzdiagramm erstellen.
- Ein Objektdiagramm erstellen.
