2.0 🚧 K-nächste-Nachbarn (K-NN) (k-nearest-neighbours)

Die Trainings-Daten werden in einem n-dimensionalen Vektorraum angeordnet und sind klassifiziert (Datenpunkte mit Klassifizierung, Label) -> überwachtes Lernen. Die Dimension n des Vektorraums ist die Anzahl der Attribute der Entitäten, Beispiele:
- Pflanzenblätter: (Länge,Breite)->Klassifizierung: Planzenart
- Ausfall einer Pumpe: (Laufzeit,Durchschnittliche Drehzahl)->Klassifizierung: Kaputt? (ja,nein)
Um bei einem neuen Datenpunkt die Klassifizierung voraussagen zu können werden die k-nächsten Nachbarn im Vektorraum ermittelt (Distanzmaß, Metrik) und aus deren mehrheitlichen Klassifizierungen die wahrscheinliche Klassifizierung des Datenpunktes bestimmt. Die k nächsten Nachbarn bestimmen die Zugehörigkeit zur Klasse.

Lesen: https://www.tecislava.com/blog/k-nearest-neighbor🔗 Aufgabe machen: https://www.tecislava.com/blog/ubung-k-nearest-neighbor🔗
Umfangreiche Beschreibung: [www.ibm.com/de-de/topics/knn 🔗]

Weiterer möglicher Einstieg mit dem Demonstrator: https://klassenkarte.de/index.php/ki/zum/🔗

Sehr anschaulich mit Java-Programm

Auf der KI-Fortbildung hat uns Siegmar von Detten eine prima k-NN-Java-Visualisierung gezeigt, folgender Code wurde durch seine Software inspiriert.

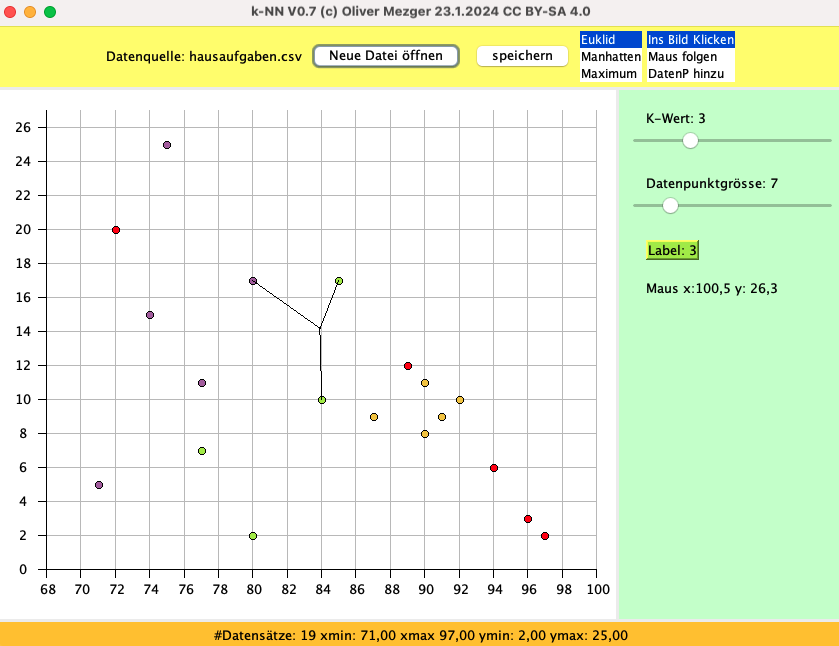
Diese Software ist noch lange nicht “schön” nach meinem Empfinden, aber ich muss “liefern” damit ich dem Bildungsplan hinterher komme…

Der Code dient zu Unterrichtszwecken und soll “zwangsarm” verbessert werden können, daher unter CC BY-SA und nicht unter GPL lizensiert, bei GPL hätten Veränderungen dokumentiert werden müssen:

KI-2001-k_NN_MM_V07.zip Herunterladen

ToDo:

Zustands-Lösung für Oberfläche, Zustandsdiagramm.
Sauberes OOP-Klassendiagramm und SuS-Aufgaben zum Code: Sequenzdiagramme 🫥..
Labels können String-Namen erhalten
Datenpunkte löschen können
Daten normalisieren..
Testdaten durchrechnen lassen..

Begriffe und Einstellungen erklärt

Laden Sie das Java-Programm und starten Sie es in Ihrer Entwicklungsumgebung, z.B. BlueJ.

Beim Start wird der Datensatz daten.csv geladen und angezeigt. Ich weis nicht was das für Daten sind. Ich behaupte einfach es sind die Längen und Breiten von Blütenblättern und die Label geben die Pflanzenart an.

Wenn nun ein neues Blütenblatt bestimmt werden soll klickt man einfach auf die Länge-Breite-Position und die k-nächsten-Nachbarn (Datenpunkte) werden bestimmt (voreingestellt sind k=3 Nachbarn) und die Mehrheit dieser Labels bestimmt das Label für das neue Blatt.

Mit Maus folgen können die Nachbarn der Mausposition fließend beobachtet werden. Mit Datenpunktgrösse kann die Darstellungsgrösse der Datenpunkte geändert werden.

Der Einfluss der Abstandsfunktion und des k-Werts wird nun beleuchtet.

2,0;2,0;1
5,0;6,0;1
7,0;8,0;1
5,0;2,0;1
4,0;2,0;1
3,0;1,0;1
10,0;10,0;2
13,0;9,0;2
13,0;4,0;3
12,0;5,0;4
15,0;1,0;4
15,0;7,0;3
13,0;8,0;3
12,0;2,0;4
10,1;3,9;4
10,0;2,0;4
12,0;1,0;4
3,0;9,0;6
2,0;8,0;6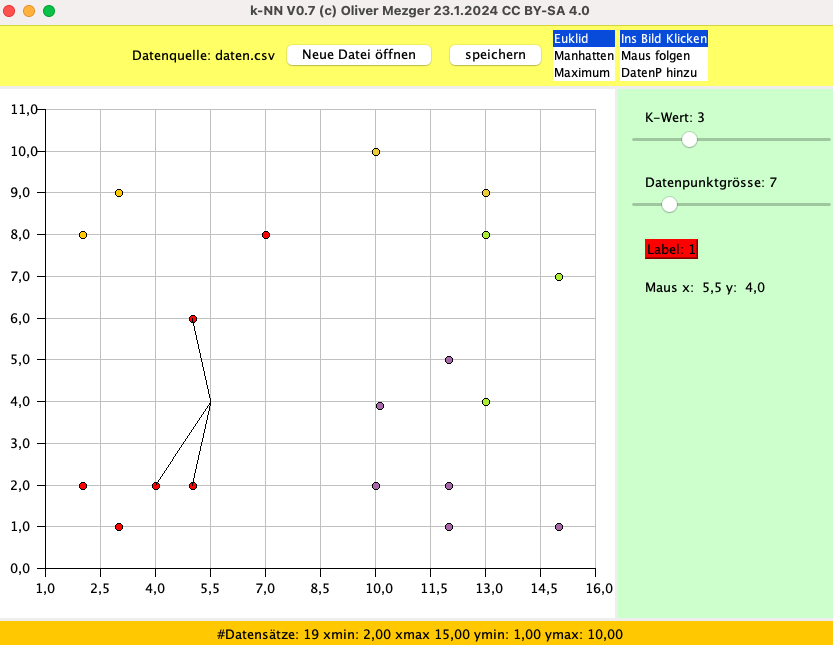

Abstandsfunktionen, Distanzmaß, Metrik

Wie weit bin ich von einem anderen Punkt entfernt? Wie Nah ist mir ein Nachbar? Gibt es da Unterschiede?
Wie weit sind zwei Punkte in einem n-dimensionalen-Vektrorraum von einander entfernt?
Ich bin noch nicht aufgeklärt, welche der Distanzmaße die sinnvollste ist. Kann mir die Vielfalt der Distanzmaße nur durch den Rechenaufwand zur Bestimmung erklären.

Luftlinie: Euklidische Distanz

Ich kann mich frei im Raum bewegen und die Entfernung ist die Luftlinie. Formel siehe Forsa.

Gerastert: Manhattan, Taxidistanz

Mit Hochhäusern dazwischen kann ich nur auf Straßen im Raster gehen, Manhattan, Mannheim. Formel siehe Forsa.

Das Maximum der Distanzen der jeweiligen Dimension

Schau die in jeder Dimension (z.B. x,y,z) die Distanz darin an und nimm das Maximum.

Aufgabenmuster

Berechne zu verschieden Punktepaaren (n-Dimensionen) die jeweilige Distanz aus..

Den Wert von k ermitteln wie viele Nachbarn sollen es sein?

Toll: k=1 ist doof weil nur der nächste Nachbar zählt, kann aber ein Ausreißer sein. Ein zu großes k kann auch wieder falsche Aussagen liefern. Es wird empfohlen mit guten Testdaten die Vorhersage für verschiedene k zu ermitteln und dann den besten k-Wert zu wählen.

Wichtige Begriffe des maschinellen Lernens

Gelabelte Daten, klassifizierte Daten: Gelabelte Daten sind Daten, die bereits einer Klasse zugeordnet sind.
Trainingsdaten: Gelabelte Daten, mit denen der Algorithmus trainiert wird.
- Besonderheit: Beim k-nächste-Nachbarn Verfahren wird der Algorithmus nicht trainiert, die Trainingsdaten werden direkt zur Vorhersage der Klasse eines neuen Datenpunkts verwendet. Aus diesem Grund wird der Algorithmus auch als lazy learner bezeichnet.
Testdaten: Um eine Aussage über die Qualität des k-nächste-Nachbarn Verfahren machen zu können, muss der Algorithmus mit sogenannten Testdaten überprüft werden. Die Testdaten sind wie die Trainingsdaten gelabelt. Für jeden einzelne Datenpunkt der Testdaten wird mit dem k-nächste-Nachbarn Verfahren eine Klasse, die Vorhersage, berechnet und diese mit dem Label an dem Testdatenpunkt verglichen. Stimmt die Vorhersage mit dem Label überein, so wurde der Testdatenpunkt richtig klassifiziert. Die Qualität des k-nächste-Nachbarn Verfahren ist dann von der Fehlerquote der klassifizierten Testdaten abhängig.
Ausreißer: Ein Ausreißer ist ein Datenpunkt, der einer Klasse zugeordnet ist, die eigentlich nicht zu erwarten wäre oder sehr ungewöhnlich ist. Ausreißer können z.B. durch Messfehler, fehlerhafte Daten, ungewöhnliche Ereignisse oder echte Abweichungen entstehen.