1.2 Schaltnetze Grundlagen
Logische Grundfunkionen
| Name | Gleichungsdarstellung | LaTex Ausdruck |
|---|---|---|
| NOT | $ Y = \overline A $ Y = ! A $ Y = \neg A $ | Y = \overline A Y = \neg A |
| AND | $ Y = A \wedge B $ Y = A & B Y = AB | Y = A \wedge B Y = A \land B |
| NAND | $ Y = \overline {A \wedge B} $ Y = !(A & B) | Y = \overline {A \wedge B} |
| OR | $ Y = A \vee B $ Y = A # B | Y = A \vee B Y = A \lor B |
Hier fehlen noch Bilder, Funktionstabellen usw. Für SuS Forsa Seite 10 anschauen.
Warum sind die Tabellen nicht A,B;Y sondern B,A;Y aufgebaut?
Ausserdem fehlt noch die Einführung mit Anton, Bert, Clara und Tresor-Beispiel usw.
Simulatorsoftware Digital
Ich verwende den Digitalsimulator Digital von Helmut Neemann. Es wird ein Java fähiges Gerät benötigt.
| B | A | AND | NAND | OR | NOR |
|---|---|---|---|---|---|
| 0 | 0 | ||||
| 0 | 1 | ||||
| 1 | 0 | ||||
| 1 | 1 |
Fülle die Tabelle aus und schreibe die 4 Gleichungen für die Schaltungen auf.
Mit den SuS in Digital aufbauen und mit “Analyse” Tabelle und Gleichungen erzeugen und mit ihrer Lösung vergleichen.
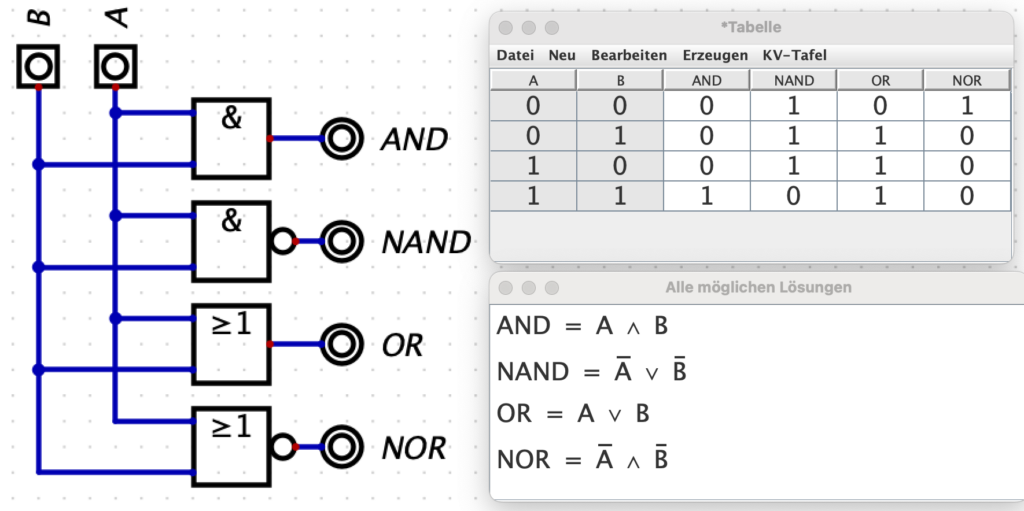
Sieht nicht wie erwartet aus? Warum? -> Ausgabereihenfolge ändern, OK.
Was passiert wenn aus Tabelle Schaltung erzeugt wird?
Warum sieht die Lösung so aus?
Programmierbare Logik Bausteine mit Disjunktiver Normal Form (DNF)
Achtung Geschichte! In jungen Jahren habe ich mit den damals käuflichen einzelnen Logik-Bausteinen meine Schaltungen zusammen gebaut Beispiele: [Elektronischer Würfel] [Reclam] [mAh-Zähler]. Durch den Fortschritt bei den programmierbaren Speichern wurden auch programmierbare Logik-Bausteine möglich. D.h. statt eine Schaltung aus vielen einzelnen Chips zusammen zu löten konnte ein Chip mit der gewünschten Funktion programmiert werden. Programmierbare Logik-Bausteine sind so aufgebaut, dass ein Eingang direkt oder invertiert in ein Und-Baustein geschaltet werden kann, die Und-Bausteine einer Gruppe werden dann in einem Oder zusammengefasst. Im alten Bildungsplan wurde damit sogar Digitaltechnik unterrichtet. Leider sind die Bausteine teuer und die Entwicklung umständlich für die meisten Anwendungen, nur wenn es schnell bei der Signalverarbeitung gehen muss macht der Aufwand damit Sinn. Für unsere Belange reichen Standart-Computer bzw. Mikrocontroller i.d.R. aus.
Die Digital-Software ist allerdings auch dafür gedacht Code für die Programmierung von Logik Bausteinen zu erzeugen, daher sind die Ergebnisse in der dafür passenden (minimierten) Form: Disjunktive Normal Form (DNF)
Disjunktive Normal Form (DNF)
Fummel das so hin, dass:
- Eingänge direkt oder invertiert in ein UND gehen
- Die Ausgänge der Unds in ein ODER am Ende gehen
Bei NAND und NOR wäre am Ausgang noch ein NOT, das geht nicht, also wird umgewandelt:
$ NAND = \overline {B \wedge A} = \overline B \vee \overline A $
$ NOR = \overline {B \vee A} = \overline B \wedge \overline A $
Stimmt das? Wie kann ich das überprüfen? Erstelle Tabelle und gehe alle Kombinationen durch.
Gibt es da nicht ein paar “Rechenregeln”?
Boolsche Algebra, Rechenregeln fürs Vereinfachen und Umwandeln
Siehe Vereinfachen von Gleichungen
Von Tabelle in DNF XOR und XNOR in DNF
Wie krieg ich minimalste Schaltung in DNF bequem hin?
Old School: Vereinfachen mit KV-Diagramm, das Prinzip der Minimierung verstehen:
KV mit 2 Eingängen
KV mit 3 Eingängen
Aufgabenmuster Übungen
Schaltung analysieren und in DNF umwandeln
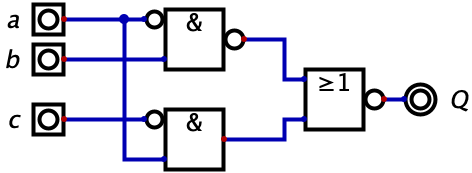
Erstelle Funktionsgleichung aus Schaltplan.
Gleichung
$Q = \overline {\overline {\overline a \wedge b} \vee \overline c \wedge a} $
Ist die Funktionsgleichung in DNF, warum nicht?
Erstelle Funktionstabelle aus Schaltplan. Reihenfolge der Eingänge a,b,c
Überprüfe deine Lösung mit der Analysefunktion von Digital.
Funktionstabelle
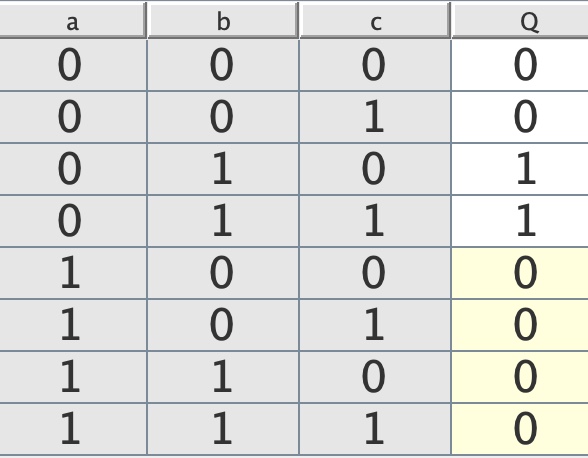
Fülle KV-Diagramm aus und ermittle daraus minimale Schaltung in DNF.
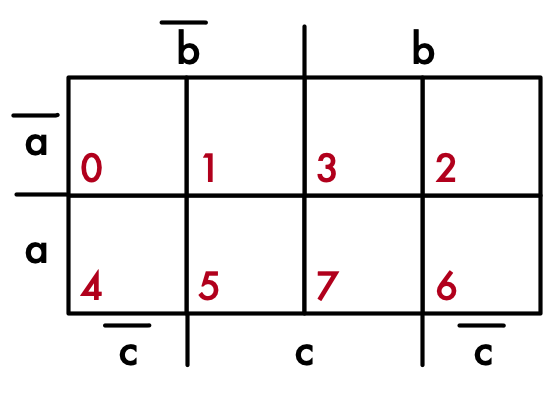
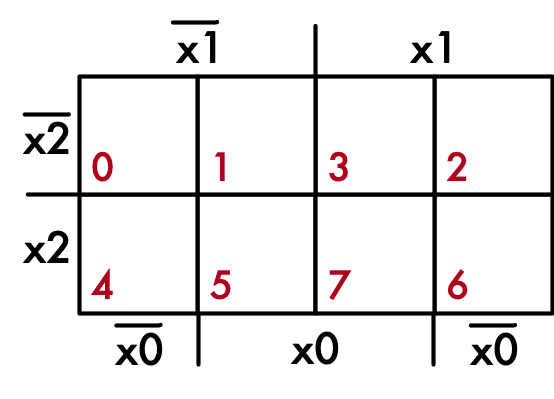
Überprüfe deine Lösung mit der KV-Funktion von Digital.
Gleichung vereinfachen
Gegebene Gleichung: $ y = (x2 \vee \overline x1) \vee (x1 \wedge \overline x0) $
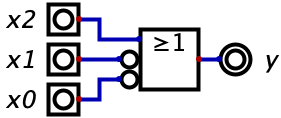
Erstelle Schaltplan.
Lösungsvorschlag:
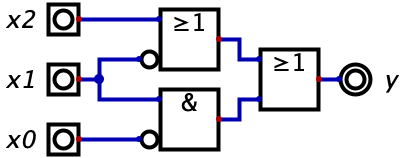
Erstelle Funktionstabelle mit Überschrift DZ,x2,x1,x0 | y .
Lösungsvorschlag:
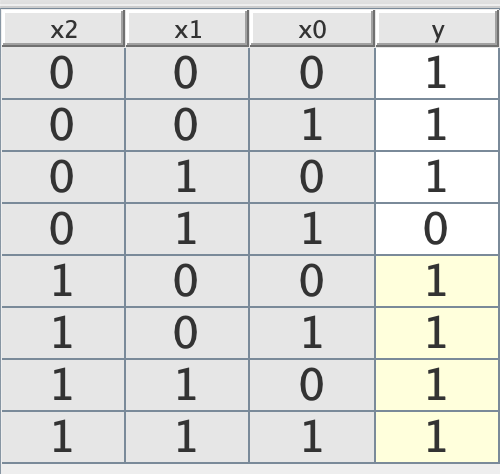
Minimiere mit KV-Diagramm und erstelle Funktionsgleichung für y.
Lösungsvorschlag:
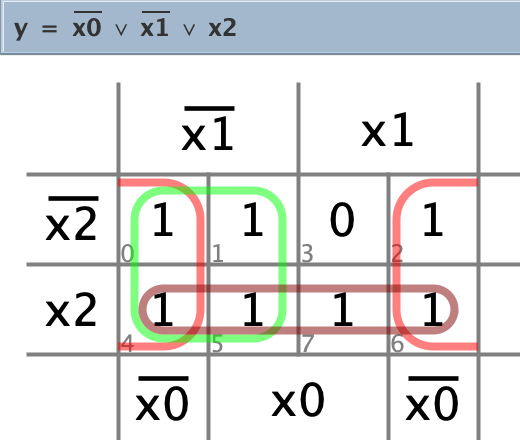
Zeichne minimierten Schaltplan.
Lösungsvorschlag:
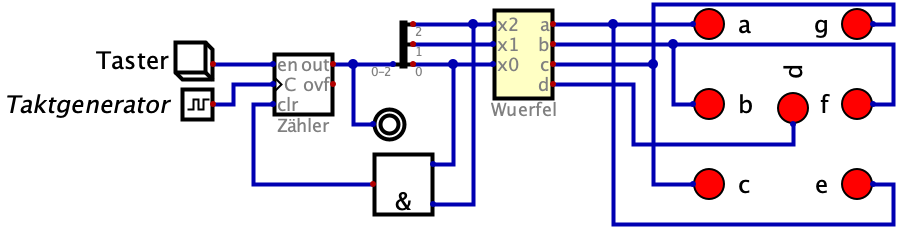
Elektronischer Würfel (KV mit Don’t Care)
Ein elektronischer Würfel soll entwickelt werden. Es gibt 6 Würfelbilder bei dem die LED a..g entsprechend leuchten sollen. Beim Drücken einer Taste soll ein Zähler ganz schnell die Dualzahlen 0 bis 5 durchzählen und bei Loslassen bleibt eine Zahl stehen. Ein Schaltnetz wandelt die Dualzahl 0..5 in das Würfelbild um. Wir erstellen zuerst eine Funktionstabelle für die Umwandlung der Dualzahl in die LED-Ansteuerung.
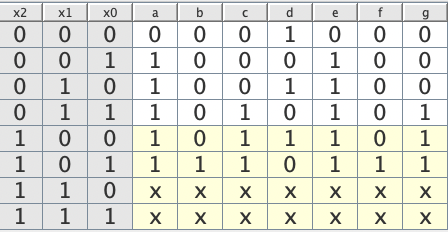
Die Zustände 6 und 7 werden nicht benötigt und die Ausgaben können als Don’t care mit einem x gekennzeichnet werden, dies ermöglicht eine bessere Minimierung, die xe wirken dabei als “Joker”. Ausserdem fällt auf, dass die Ausgänge e, f, g die selben Werte wie a, b, c ausgeben: a = e, b = f, c = g. Also reicht ein Schaltnetz für a..d.
Wir erstellen die KV-Diagramme und Gleichungen für a, b, c, d.
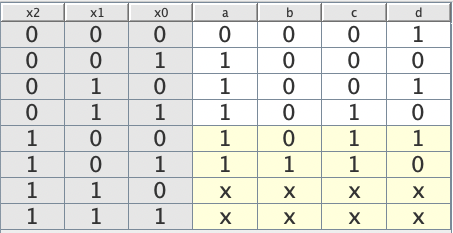
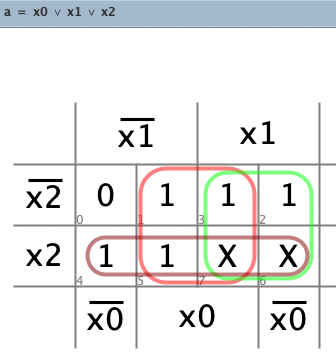
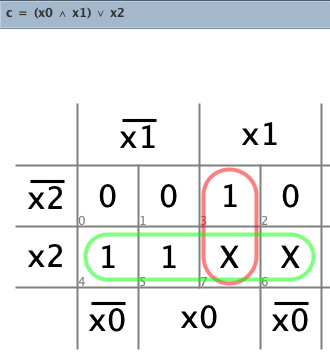

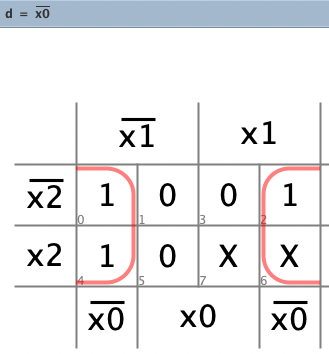
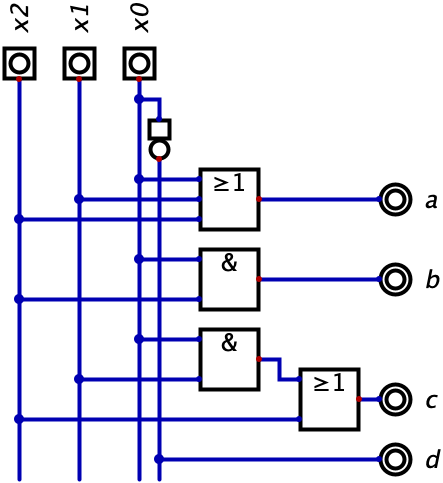
Die erzeugte Schaltung unter dem Namen “Wuerfel.dig” abspeichern. Zum Testen erzeugen wir eine neue Schaltung und wählen Würfel als benutzerdefiniertes Bauteil aus:
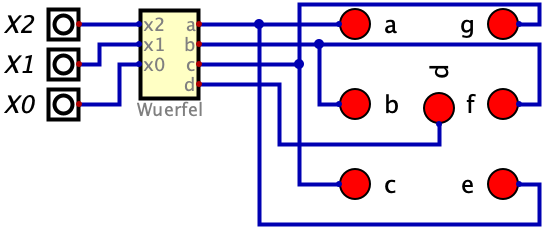
Richtig würfeln mit Takt und Zähler
Um damit richtig zu würfeln fehlt noch ein Zähler von 0 bis 5. In Digital gibt es unter Bauteile->Speicher einen Zähler. Der hat aber zunächst nur einen Ausgang und ist nur 1 Bit breit, kann also nur 0<->1 zählen. Mit der rechten Maustaste kann er auf 3 Bit erweitert werden. Leider hat er dann aber immer noch nur einen Ausgang out, aber dieser ist jetzt nicht mehr eine einzelne Leitung sondern ein Leitungsbündel. Um aus diesem Bündel wieder einzelne Leitungen zu bekommen gibt es ein Splitter/Merger-Bauteil unter Bauteile->Leitungen. Mit einem Taster am Enable-Eingang en des Zählers kann gesteuert werden ob der Zähler zählen soll: Er zählt nur wenn der Taster gedrückt ist. Ein Taktgenerator am Clock-Eingang c gibt die Frequenz vor mit der gezählt werden soll, wenn sie hoch genug ist >500 Hz wird so schnell gezählt, dass damit durch einen Menschen als Tastendrücker ein zufälliger Wert beim Loslassen erzeugt wird. Ein 3Bit-Zähler zählt von 0 bis 7, wir brauchen aber einen Zähler von 0 bis 5! Praktischerweise gibt es einen Clear-Eingang clr, mit dem der Zähler auf 0 zurückgesetzt werden kann. Ist clr 1 wird bei der nächsten steigenden Taktflanke auf 0 gesprungen. Mit dem Und wird der clr-Eingang beim Wert 5 auf 1 gesetzt, also nach 5 kommt dann nicht 6 sondern 0. Wie so ein Zähler funktioniert und innen drin aufgebaut ist lernen wir bei den Schaltwerken.
Aufgabe Schadstoffkonzentrationsanzeige
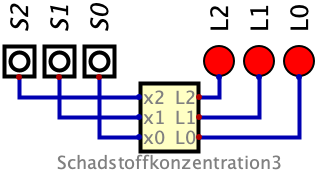
Für eine Schadstoffkonzentrationsanzeige soll ein Schaltnetz erstellt werden. Sensoren S0..S2 geben eine 1 aus, wenn sie Schadstoffe erkennen. Ein Leuchtband aus LED L0..L2 gibt die Anzahl der schadstoffmessenden Sensoren S0..S2 aus. Gibt kein Sensor Alarm leuchtet keine LED, bei einem Sensor leuchtet L0, bei zwei Sensoren L0 und L1, bei allen drei Sensoren leuchten L0, L1 und L2.
- Erstellen Sie eine Funktionstabelle.
- Entwickeln Sie mit KV-Diagrammen die Gleichungen für L0..L2
- Erstellen Sie das Schaltnetz mit Digital und speichern es unter Schadstoffkonzentration3.dig ab.
- Laden Sie die Testschaltung Ti-1280-Schadstoffkonzentration3-Aufg.dig und testen Sie ihre Lösung.
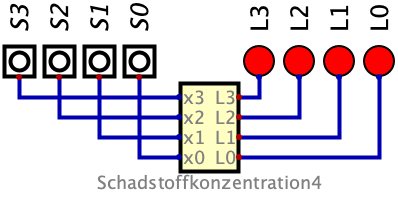
Schadstoffkonzentrationsanzeige mit 4 Sensoren
Die Schadstoffkonzentrationsanzeige soll auf 4 Sensoren erweitert werden. Entwickeln und testen Sie Ihre Lösung.
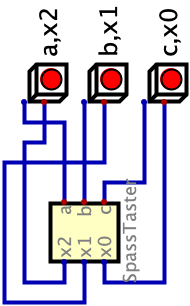
Aufgabe: Spass-Taster
Drei Taster x2..x0 mit eingebauter LED a..c können gedrückt werden. Normalerweise wird erwartet, dass die eingebaute LED dann leuchtet. Hier soll zum Spass aber wenn man auf einen Taster drückt ausgerechnet die die anderen zwei Taster leuchten. Es kann immer nur ein Taster gedrückt werden (Don’t care Zustände!)
Erstellen Sie eine Funktionstabelle und die KV-Diagramme.
Erstellen Sie die Schaltung SpassTaste.dig und testen Sie sie mit der Vorgabe. Notfall-Lösung:
Aufgabe: Kreislicht
Ein Kreis aus 6 LED soll sich im und gegen den Uhrzeigersinn drehen. Bei x2=0 dreht es sich im und bei x2=1 gegen den Uhrzeigersinn. Der Zähler zählt 0,1,2,0 usw. Dabei werden die Ausgänge a..c nacheinander auf 1 geschaltet. Der Zustand 3 des Zählers kann als Don’t care verwendet werden.
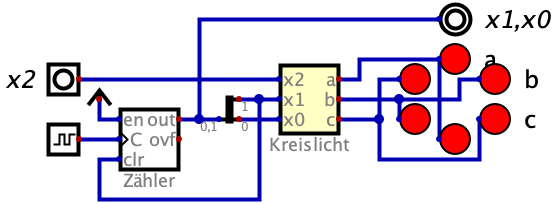
Erstellen Sie eine Funktionstabelle für das Kreislicht.
Minimieren Sie die Schaltfunktion mit KV-Diagrammen.
Erstellen Sie das Schaltnetz und testen Sie Ihren Entwurf mit der Vorgabe.
Notfall-Lösung:
